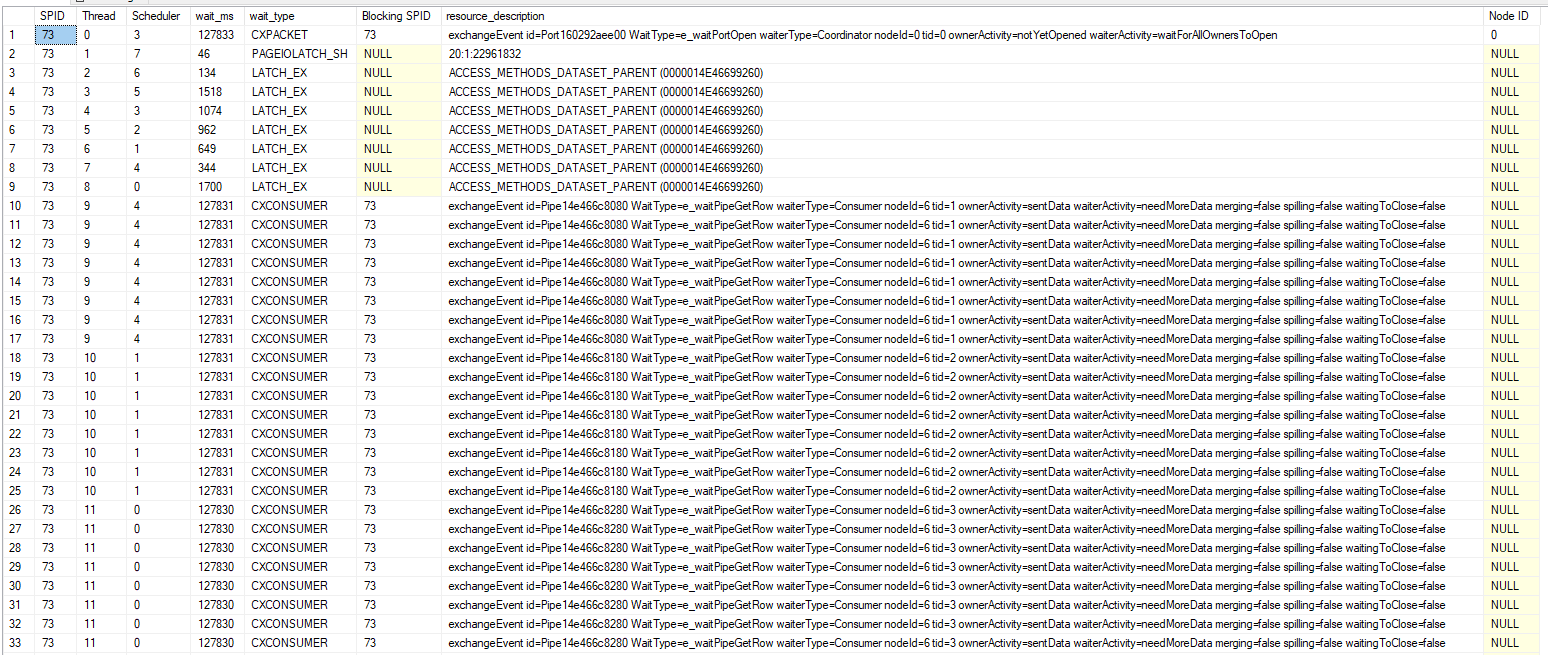
Itzik Ben-Gan posted an interesting T-SQL challenge on SQL performance dot com. I’m writing up my solution in my own blog post because I have a lot to say and getting code formatting right can be tricky in blog post comments. For reference, my test machine is using SQL Server 2019 CU14 with an i7-9700K CPU @ 3.60 GHz processor. The baseline cursor solution completes in 8465 ms on my machine.
Running Totals
A simple way to solve this problem is to calculate running totals of quantity separately for supply and demand, treat the resulting rows as intervals, and find the intersections between supply and demand intervals. It is fairly straightforward and fast to calculate the interval start and end points and load them into temp tables, so I’ll omit that code for now. We can find the intersecting intervals with the query below( which you should not run):
SELECT d.ID DemandId, s.ID as SupplyID,
CASE
WHEN d.IntervalEnd >= s.IntervalEnd THEN s.IntervalEnd - CASE WHEN s.IntervalStart >= d.IntervalStart THEN s.IntervalStart ELSE d.IntervalStart END
ELSE d.IntervalEnd - CASE WHEN s.IntervalStart >= d.IntervalStart THEN s.IntervalStart ELSE d.IntervalStart END
END TradeQuantity
FROM #demand_intervals d
CROSS JOIN #supply_intervals s
WHERE d.IntervalEnd > s.IntervalStart AND d.IntervalStart < s.IntervalEnd
OPTION (QueryRuleOff BuildSpool);
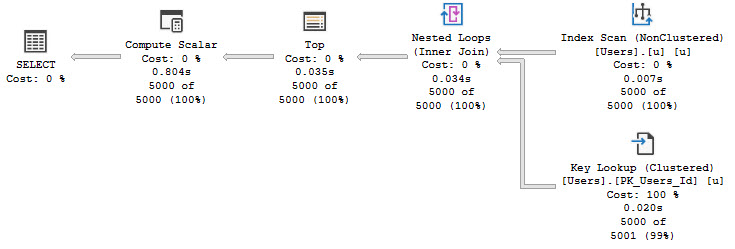
Performance is terrible for this query because there is no possible index that will make that join condition fast. The query takes 955 seconds of CPU time and 134 seconds of elapsed time at MAXDOP 8.
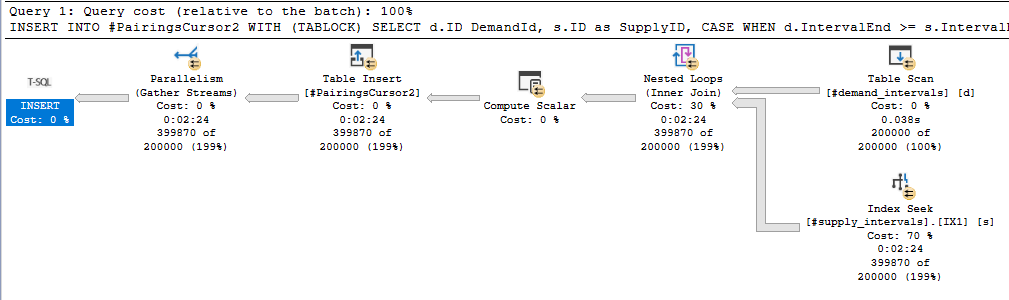
This blog post is about batch mode, so we need to turn that nested loop join into a hash join. It is important to recall that a hash join requires at least one equality condition in the join clause.
Exploring the Data
It’s important to Know Your Data while query writing, especially if you want to cheat in a performance competition. Taking a quick look at the Auctions table with the 400k row configuration:

The things that stand out to me are that there are an equal number of supply and demand rows, both supply and demand have nearly the same average value, and the maximum quantity for both supply and demand is under 100. We can exploit the relatively low maximum quantity value to improve performance. A supply interval with a end point that is more than 100 units away from the demand end point cannot possibly intersect it. This is one of those things that feels intuitively correct, but I’ll go ahead and prove it anyway by contradiction.
Suppose that 100 is the maximum interval length, [d_start, d_end] and [s_start, s_end] overlap, s_end is more than 100 units away from d_end.
- The distance between end points implies that d_end < s_end – 100
- If they overlap, then s_start < d_end
- This implies that s_start < d_end < s_end – 100
- This implies that s_start < s_end – 100
- This implies that s_end – s_start > 100
The final statement is impossible because 100 is the maximum interval length. You can do the same proof in the other direction. Therefore, it should be safe to add some filters to our original query:
SELECT d.ID DemandId, s.ID as SupplyID,
CASE
WHEN d.IntervalEnd >= s.IntervalEnd THEN s.IntervalEnd - CASE WHEN s.IntervalStart >= d.IntervalStart THEN s.IntervalStart ELSE d.IntervalStart END
ELSE d.IntervalEnd - CASE WHEN s.IntervalStart >= d.IntervalStart THEN s.IntervalStart ELSE d.IntervalStart END
END TradeQuantity
FROM #demand_intervals d WITH (TABLOCK)
CROSS JOIN #supply_intervals s WITH (TABLOCK)
WHERE d.IntervalEnd > s.IntervalStart AND d.IntervalStart < s.IntervalEnd
AND s.IntervalEnd >= d.IntervalEnd - 100
AND s.IntervalEnd <= d.IntervalEnd + 100;
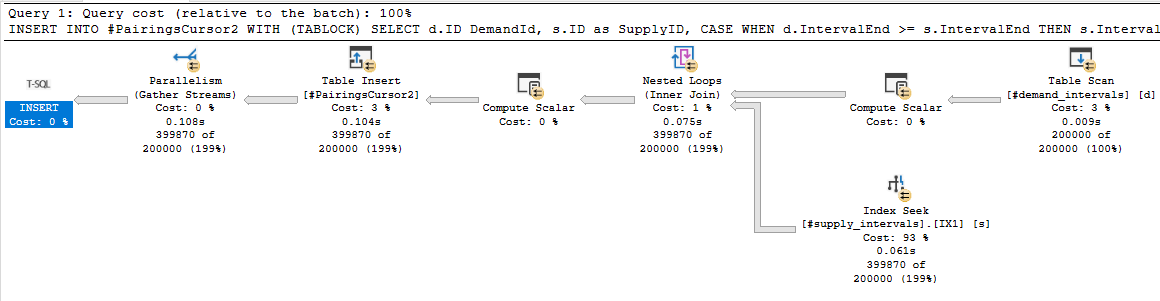
Now we can get a proper index seek on the s.IntervalEnd column. Performance is significantly better with this additional filter clause. The total runtimes for all steps, including the omitted temp table creation, are 1030 ms of CPU time and 345 ms of elapsed time. We are of course not using batch mode though:
Buckets
Time for more math. Starting with the following filter conditions:
AND s.IntervalEnd >= d.IntervalEnd – 100
AND s.IntervalEnd <= d.IntervalEnd + 100;
I can divide both sides by 100 and the condition will still be true:
AND s.IntervalEnd / 100 >= d.IntervalEnd / 100 – 1
AND s.IntervalEnd / 100 <= d.IntervalEnd / 100 + 1
You’ll have to take my word for it that the equation is still true if we truncate everything down to integers:
AND FLOOR(s.IntervalEnd / 100) >= FLOOR(d.IntervalEnd / 100) – 1
AND FLOOR(s.IntervalEnd / 100) <= FLOOR(d.IntervalEnd / 100) + 1
Now we’re dealing with integers, so we can express this as the following:
FLOOR(s.IntervalEnd / 100) IN (FLOOR(d.IntervalEnd / 100) – 1, FLOOR(d.IntervalEnd / 100) + 0, FLOOR(d.IntervalEnd / 100) + 1)
Rewriting once again:
FLOOR(s.IntervalEnd / 100) = FLOOR(d.IntervalEnd / 100) – 1
OR FLOOR(s.IntervalEnd / 100) = FLOOR(d.IntervalEnd / 100) + 0
OR FLOOR(s.IntervalEnd / 100) = FLOOR(d.IntervalEnd / 100) + 1
That’s still not eligible for a hash join, but it is if we change it to a UNION ALL:
... JOIN ON ...
FLOOR(s.IntervalEnd / 100) = FLOOR(d.IntervalEnd / 100) - 1
UNION ALL
... JOIN ON ...
FLOOR(s.IntervalEnd / 100) = FLOOR(d.IntervalEnd / 100) + 0
UNION ALL
... JOIN ON ...
FLOOR(s.IntervalEnd / 100) = FLOOR(d.IntervalEnd / 100) + 1
We have successfully transformed a single BETWEEN join filter into three joins with equality filters. All three of those joins are eligible for batch mode.
A visual representation may be helpful. Suppose we have two demand intervals that end in 150.2 and 298.2. We need to match those intervals with 8 supply intervals with end points that range from 1.1 to 399.1. To do so, we can divide the intervals into buckets of 100 width and join on matching bucket values as well as the immediately adjacent bucket values:
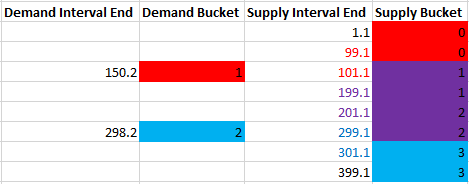
The demand interval that ends in 150.2 has a bucket value of 1, so it is matched with supply buckets 0, 1, and 2. In this way, we can guarantee that any supply interval that’s 100 or fewer units away ends up getting matched with the right demand intervals. The supply buckets with a background of red are only matched to the demand interval of 150.2, blue is only matched to the demand interval of 298.2, and purple is matched to both. The buckets are overly inclusive of course. The actual rows that might match based on distance have their font color changed in the same way, but filtering out extra rows later will be no problem. The important thing is that we have an equality condition to work with. Now that we can finally perform hash joins, it’s time to work out all of the details.
Gotta Go Fast
We need to perform three operations:
- Calculate the maximum interval length.
- Calculate running totals for supply and demand, their bucket values, and load them into temporary objects.
- Query the temp tables to load the final results into another table.
For step 1, we simply need an index on the Quantity column to make the query fast. We also need to get an exclusive lock and hold it until we’re finished with all of the steps. Otherwise the max length could change in the middle of our code’s execution.
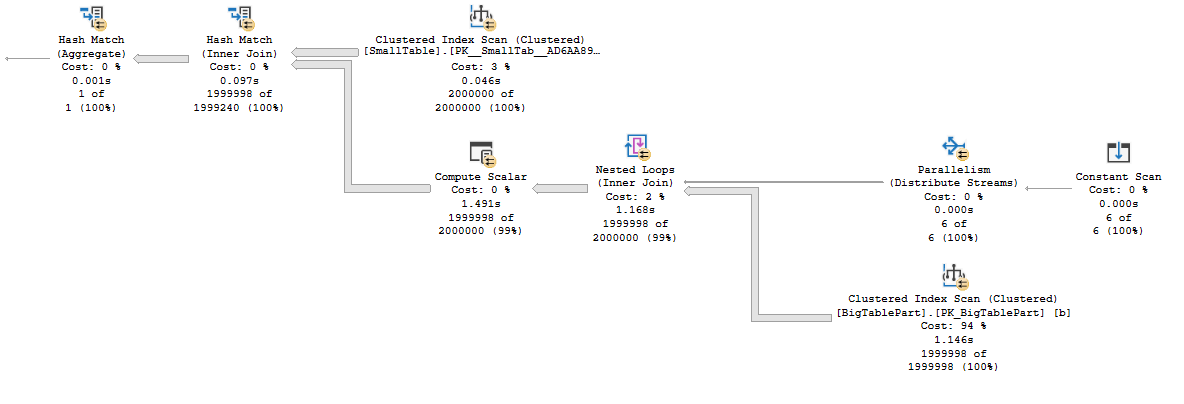
For step 2, the best performing options are either a MAXDOP 1 query with an ordered index scan and a batch mode window aggregate or a parallel query with a batch mode sort, parallel batch mode window aggregate, and parallel insert. An NCCI on the Auctions table is helpful in getting batch mode. In order to make the code go as fast as possible, I elected to use the parallel option at MAXDOP 4 even though it uses significantly more CPU time than the MAXDOP 1 option. DOP is at 4 instead of 8 due to contention caused by the NESTING_TRANSACTION_FULL latch. Here’s an estimated plan picture in case you don’t know what I mean by all of that:

For the third query, I’m using a UNION ALL of 3 joins that are eligible for batch mode like I said earlier. I added some query hints to reduce compile time.
As a step 0 that I forgot to mention earlier, create the following indexes on the Auctions table:
CREATE INDEX IX_Auctions__Code_ID__INCLUDE_Quantity ON Auctions (Code, ID) INCLUDE (Quantity);
CREATE INDEX IX_Auctions__Quantity ON Auctions (Quantity);
CREATE NONCLUSTERED COLUMNSTORE INDEX NCCI_Auctions ON Auctions (Code) with (MAXDOP = 1);
You can find the full code below for all three steps:
SET NOCOUNT ON;
DROP TABLE IF EXISTS #PairingsCursor2;
CREATE TABLE #PairingsCursor2
(
DemandID INT NOT NULL,
SupplyID INT NOT NULL,
TradeQuantity DECIMAL(19, 6) NOT NULL
);
DROP TABLE IF EXISTS #demand_intervals;
CREATE TABLE #demand_intervals (
ID INT NOT NULL,
IntervalStart DECIMAL(19, 6) NOT NULL,
IntervalEnd DECIMAL(19, 6) NOT NULL,
IntervalBucket BIGINT NOT NULL
);
DROP TABLE IF EXISTS #supply_intervals;
CREATE TABLE #supply_intervals (
ID INT NOT NULL,
IntervalStart DECIMAL(19, 6) NOT NULL,
IntervalEnd DECIMAL(19, 6) NOT NULL,
IntervalBucket BIGINT NOT NULL
);
DECLARE @MaxQuantityRange DECIMAL(19, 6);
BEGIN TRANSACTION;
SELECT @MaxQuantityRange = MAX(Quantity) - MIN(Quantity)
FROM Auctions WITH (TABLOCKX);
INSERT INTO #demand_intervals WITH (TABLOCK)
SELECT ID, rt - Quantity IntervalStart, rt IntervalEnd, CAST(rt / @MaxQuantityRange AS BIGINT) AS IntervalBucket
FROM
(
SELECT a.ID, Quantity, SUM(Quantity) OVER (ORDER BY a.ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW) rt
FROM dbo.Auctions a WITH (TABLOCK)
WHERE Code = 'D'
) q
OPTION (USE HINT('ENABLE_PARALLEL_PLAN_PREFERENCE'), MAXDOP 4);
INSERT INTO #supply_intervals WITH (TABLOCK)
SELECT ID, rt - Quantity IntervalStart, rt IntervalEnd, CAST(rt / @MaxQuantityRange AS BIGINT) AS IntervalBucket
FROM
(
SELECT a.ID, Quantity, SUM(Quantity) OVER (ORDER BY a.ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW) rt
FROM dbo.Auctions a WITH (TABLOCK)
WHERE Code = 'S'
) q
OPTION (USE HINT('ENABLE_PARALLEL_PLAN_PREFERENCE'), MAXDOP 4);
/*
-- prevents temp table caching, slight performance overhead in last query, but avoids "expensive" stats gathering for uncached object scenario
CREATE STATISTICS s0 ON #demand_intervals (IntervalBucket) WITH SAMPLE 0 ROWS;
CREATE STATISTICS s1 ON #supply_intervals (IntervalBucket) WITH SAMPLE 0 ROWS;
*/
INSERT INTO #PairingsCursor2 WITH (TABLOCK)
SELECT d.ID DemandId, s.ID as SupplyID,
CASE
WHEN d.IntervalEnd >= s.IntervalEnd THEN s.IntervalEnd - CASE WHEN s.IntervalStart >= d.IntervalStart THEN s.IntervalStart ELSE d.IntervalStart END
ELSE d.IntervalEnd - CASE WHEN s.IntervalStart >= d.IntervalStart THEN s.IntervalStart ELSE d.IntervalStart END
END TradeQuantity
FROM #demand_intervals d WITH (TABLOCK)
INNER JOIN #supply_intervals s WITH (TABLOCK) ON d.IntervalBucket = s.IntervalBucket
WHERE d.IntervalEnd > s.IntervalStart AND d.IntervalStart < s.IntervalEnd
UNION ALL
SELECT d.ID DemandId, s.ID as SupplyID, CASE WHEN d.IntervalEnd >= s.IntervalEnd THEN s.IntervalEnd - CASE WHEN s.IntervalStart >= d.IntervalStart THEN s.IntervalStart ELSE d.IntervalStart END
ELSE d.IntervalEnd - CASE WHEN s.IntervalStart >= d.IntervalStart THEN s.IntervalStart ELSE d.IntervalStart END
END TradeQuantity
FROM #demand_intervals d WITH (TABLOCK)
INNER JOIN #supply_intervals s WITH (TABLOCK) ON s.IntervalBucket = d.IntervalBucket - 1
WHERE d.IntervalEnd > s.IntervalStart AND d.IntervalStart < s.IntervalEnd
UNION ALL
SELECT d.ID DemandId, s.ID as SupplyID, CASE WHEN d.IntervalEnd >= s.IntervalEnd THEN s.IntervalEnd - CASE WHEN s.IntervalStart >= d.IntervalStart THEN s.IntervalStart ELSE d.IntervalStart END
ELSE d.IntervalEnd - CASE WHEN s.IntervalStart >= d.IntervalStart THEN s.IntervalStart ELSE d.IntervalStart END
END TradeQuantity
FROM #demand_intervals d WITH (TABLOCK)
INNER JOIN #supply_intervals s WITH (TABLOCK) ON s.IntervalBucket = d.IntervalBucket + 1
WHERE d.IntervalEnd > s.IntervalStart AND d.IntervalStart < s.IntervalEnd
OPTION (USE HINT('ENABLE_PARALLEL_PLAN_PREFERENCE'), MAXDOP 8, HASH JOIN, CONCAT UNION, FORCE ORDER, NO_PERFORMANCE_SPOOL); -- reduce compile time
COMMIT TRANSACTION;
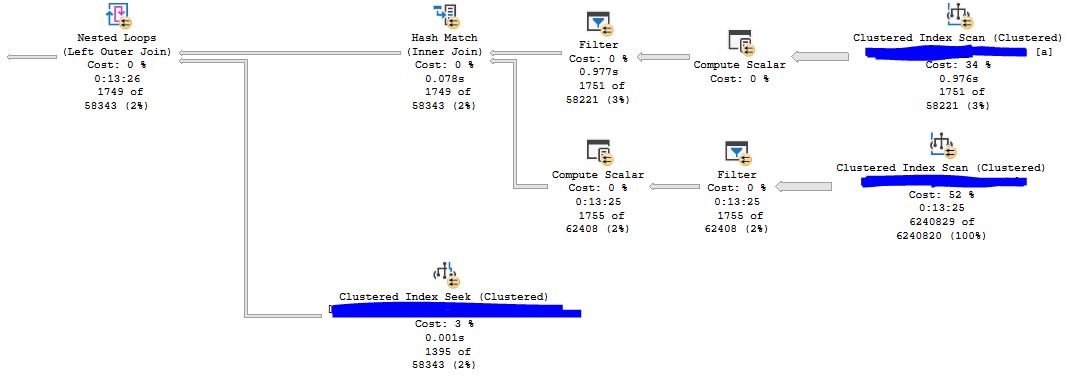
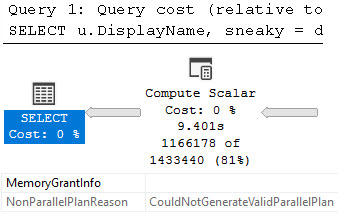
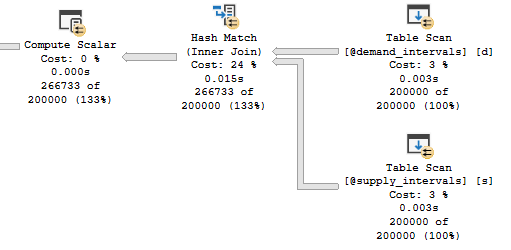
For the first execution, CPU time is generally around 1245 ms and elapsed time is around 500 ms. For subsequent executions, CPU time is around 634 ms and elapsed time is around 168 ms. Here is an actual execution plan for step 3:
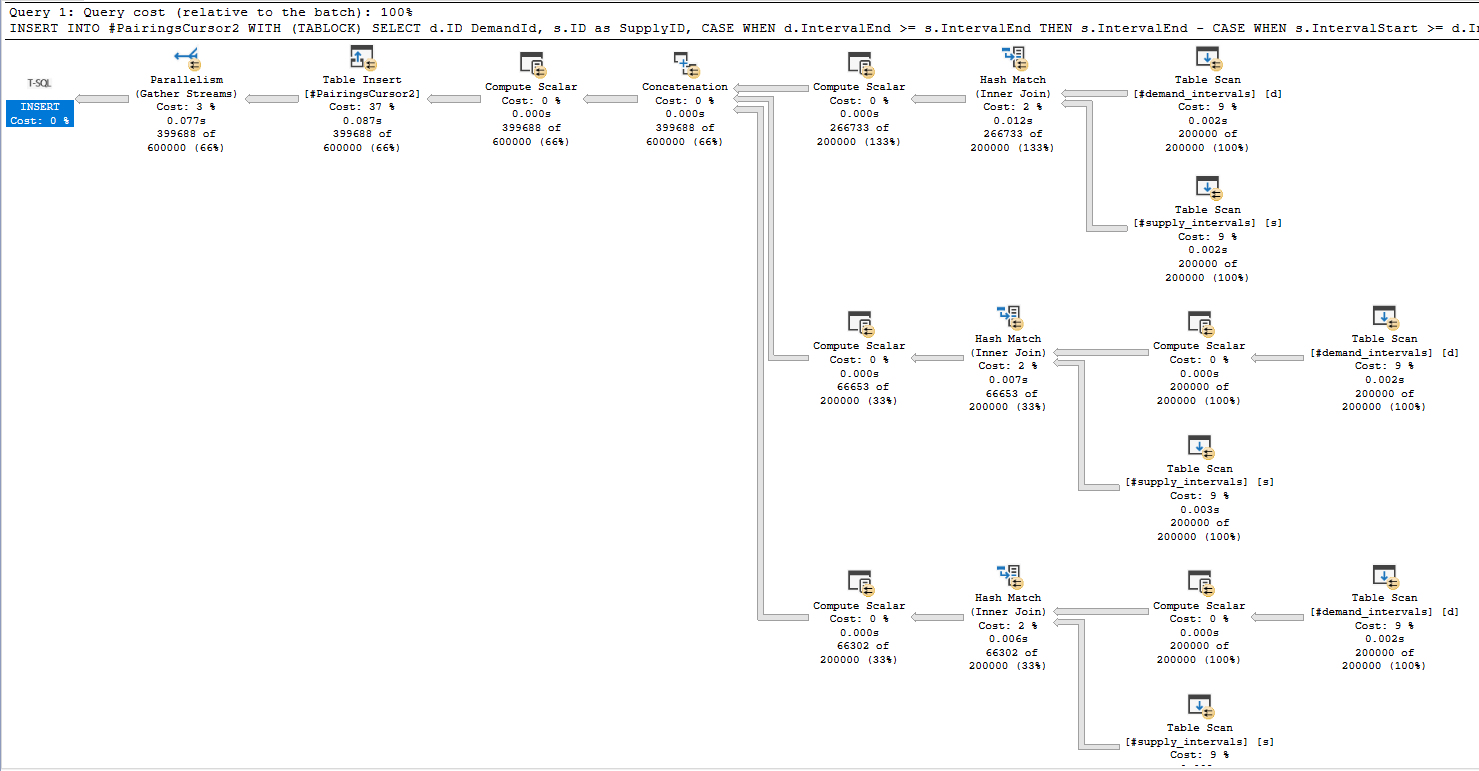
Not surprisingly, the join for matching buckets returns significantly more rows than the joins for adjacent buckets.
REEEEEEEEEEEEECOMPILES
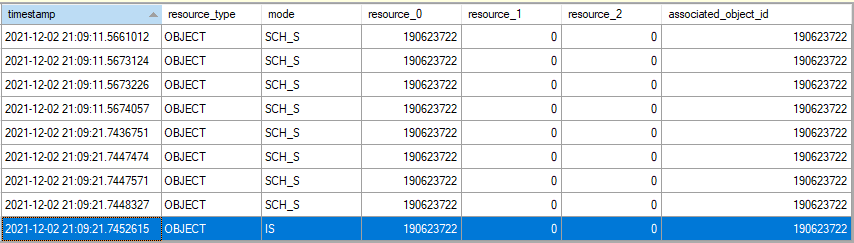
You may be wondering why the first execution takes so much longer than subsequent executions. The problem is the creation of temp table statistics. For some reason, SQL Server issues four StatMan queries per statistic that it creates:

Some of them run at MAXDOP 1 and some of them run at MAXDOP 8 and all of that time adds up. After the first execution the creation of statistics no longer happens, I assume due to statistics caching for temporary tables. Even adding an explicit FULLSCAN create statistics statement doesn’t avoid this problem for some reason. You can create 0 row statistics if you like (see the commented out code), but I’m going to declare a moral victory here instead of digging into it further. If the biggest performance problem for your query is statistics creation on a pair of 200k row temp tables then you probably have pretty efficient code.
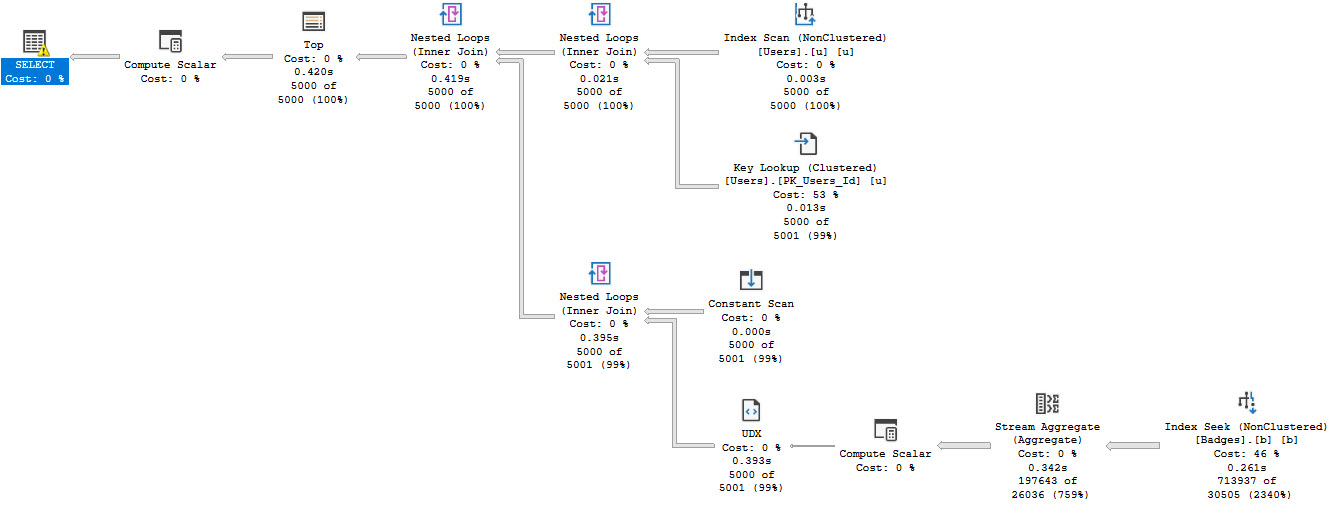
With that said, table variables are an interesting alternative here. I get consistent runtimes of 550 CPU ms and 230 ms of elapsed time using table variables. The deferred compilation feature introduced in SQL Server 2019 is important to get the right query plan. We lose a bit of runtime for the MAXDOP 1 table variable inserts and the final insert is slightly less efficient as well due to the missing statistics. Still, the runtimes are consistent between the first and second executions and overall CPU usage is down. Also you have to admit that seeing a batch mode table variable scan with a correct cardinality estimate (without RECOMPILE) is pretty cool:
Query Scaling
The performance of the batch mode query greatly depends on the maximum interval length. Query runtime increases in a roughly linear fashion as the max length increases:
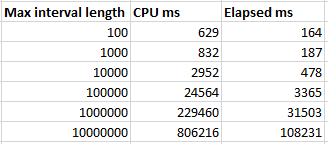
The linear pattern is broken for the final test case because all of the rows are in a single bucket at that point, so two out of three of the joins don’t do much of anything. Is this type of query safe to use in production? Sure, as long as you’re okay with significantly worse performance if a single outlier row happens to appear. Possible defenses against that include additional constraints on the data, knowing your data well, or writing a fallback algorithm if the maximum interval length is too long for the batch mode bucketizing approach to perform well.
Final Thoughts
This blog post shows how batch mode hash joins can be used as an efficient solution to find intersecting intervals, provided that the maximum interval length is sufficiently small. The important thing is everyone involved had fun. Thanks for reading!